Discover the complete guide to Charles Law, including its formula, derivation, and practical applications. In the world of physics and chemistry, gas laws play a crucial role in understanding the behavior of gases under various conditions. Among these, Charles’s Law holds significant importance. This scientific principle describes how the volume of a gas changes with temperature when pressure is held constant. Understanding this relationship helps students, researchers, and engineers in a variety of fields including meteorology, aeronautics, and thermodynamics..
Table of Contents
What is Charles’s Law?
Charles’s Law, also known as the law of volumes, states that:
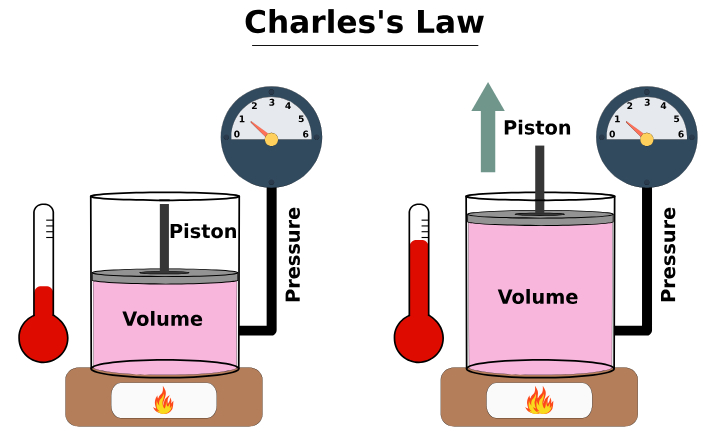
“The volume of a given mass of gas is directly proportional to its absolute temperature, provided the pressure remains constant.”
In simpler terms, as the temperature of a gas increases, its volume increases, and vice versa — but only when pressure is unchanged.
This law was first formulated by Jacques Charles, a French physicist, in the late 18th century based on experiments that observed this temperature-volume relationship.
Charles’s Law Formula
The mathematical expression of Charles’s Law is: V1T1=V2T2\frac{V_1}{T_1} = \frac{V_2}{T_2}T1V1=T2V2
Where:
- V1V_1V1 = Initial volume of the gas
- T1T_1T1 = Initial temperature (in Kelvin)
- V2V_2V2 = Final volume of the gas
- T2T_2T2 = Final temperature (in Kelvin)
It’s important to remember that temperature must always be in Kelvin (K) for this equation to work correctly, as the Kelvin scale starts from absolute zero.
Key Points of Charles Law
- Direct Proportionality: Volume increases with temperature and decreases as temperature lowers, assuming constant pressure.
- Constant Pressure: The law is only valid when the gas is not under varying pressure.
- Kelvin Scale Use: Calculations must convert Celsius to Kelvin using: K=°C+273.15K = °C + 273.15K=°C+273.15
Derivation of Charles Law
The derivation is based on empirical observations, but it can also be supported theoretically using the Ideal Gas Law: PV=nRTPV = nRTPV=nRT
If pressure PPP and number of moles nnn are constant, then: V=nRPTV = \frac{nR}{P}TV=PnRT
This shows volume VVV is directly proportional to temperature TTT, confirming Charles’s Law: V∝TV \propto TV∝T
Graphical Representation
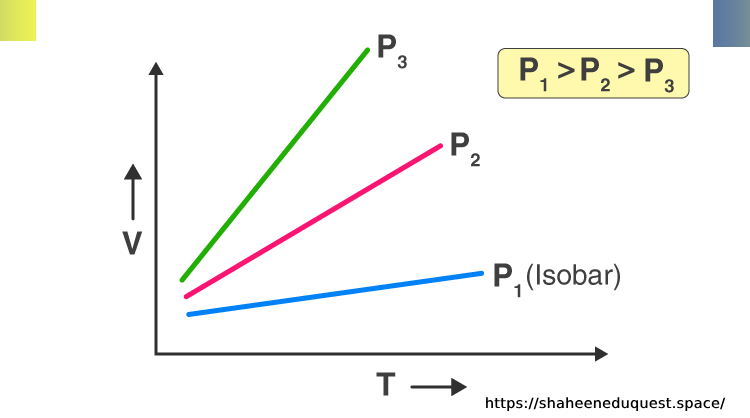
When Charles’s Law is graphed, temperature (in Kelvin) is plotted on the x-axis and volume on the y-axis. The result is a straight line that passes through the origin, illustrating a linear relationship.
Characteristics of the Graph:
- Straight line = constant rate of volume change with temperature
- Starts at absolute zero (0 K), where theoretically, the volume becomes zero
- Slope = proportionality constant depending on pressure and amount of gas
Example Problems
Example 1: Volume Expansion
A gas occupies a volume of 500 mL at 273 K. What will be its volume at 373 K (assuming constant pressure)?
Solution:
Given:
V1=500 mL, T1=273 K, T2=373 KV_1 = 500 \, \text{mL}, \, T_1 = 273 \, K, \, T_2 = 373 \, KV1=500mL,T1=273K,T2=373K
Using the formula: V1T1=V2T2\frac{V_1}{T_1} = \frac{V_2}{T_2}T1V1=T2V2 500273=V2373\frac{500}{273} = \frac{V_2}{373}273500=373V2 V2=500×373273≈683 mLV_2 = \frac{500 \times 373}{273} \approx 683 \, \text{mL}V2=273500×373≈683mL
Answer: The new volume is approximately 683 mL.
Applications of Charles Law
Charles’s Law is more than just textbook theory; it has practical applications in daily life and industry:
1. Hot Air Balloons
Hot air balloons operate based on Charles’s Law. When air inside the balloon is heated, it expands, becoming less dense than the surrounding cooler air, which causes the balloon to rise.
2. Vehicle Tires
In hot weather, the air inside car tires expands due to rising temperatures. This can increase tire pressure significantly, showing Charles’s Law in action.
3. Breathing Mechanism
In human lungs, the volume of air changes with the temperature of inhaled and exhaled air, subtly following Charles’s Law dynamics during respiration.
4. Refrigeration Systems
Refrigerators and air conditioners manipulate gas temperatures to control volume and pressure, leveraging principles from both Charles’s Law and Boyle’s Law.
Limitations of Charles Law
While Charles’s Law is extremely useful, it’s essential to understand its limitations:
- Only applicable to ideal gases; real gases may deviate slightly.
- Pressure must remain constant.
- Gases must not condense into liquids during temperature changes.
- Very low temperatures near absolute zero are theoretical, not always practical.
Difference Between Boyle’s Law and Charles’s Law
| Feature | Boyle’s Law | Charles’s Law |
|---|---|---|
| Relationship | Pressure ↔ Volume (inverse) | Volume ↔ Temperature (direct) |
| Constant Variable | Temperature | Pressure |
| Formula | P1V1=P2V2P_1V_1 = P_2V_2P1V1=P2V2 | V1T1=V2T2\frac{V_1}{T_1} = \frac{V_2}{T_2}T1V1=T2V2 |
| Graph Type | Hyperbolic curve | Straight line |
| Real-life Use | Syringes, scuba diving | Hot air balloons, tire inflation |
Conclusion
Charles Law offers critical insight into how gases behave when subjected to changes in temperature at constant pressure. Its clear, linear relationship allows for accurate predictions and practical applications in everything from balloon flights to everyday car maintenance.
Whether you’re a student studying for an exam or a curious mind diving into thermodynamics, understanding Charles’s Law equips you with foundational knowledge about gas behavior — a small part of physics that explains big things in our world.
